Contents
操作と表現
MQL4での演算と式の重要性を理解するために、特別な類推は必要ありません。 実際には、単純な算術演算や演算式と同じです。 誰もが記録していることを理解している = n + m 、メンバ f、 n 、 m は変数、符号 = と + は演算符号、 n + m は式です。
この本の前のセクションでは、さまざまな種類のデータを表示する必要性について学習しました。 ここでは、これらのデータ間の可能な関係について説明します(まだ、リンゴに平方メートルを追加することはできません)。 MQL4では、式での演算の使用規則にはいくつかの自然な制限があります。
オペランド、演算、演算記号、式の概念
オペランド は、定数、変数、配列コンポーネント、または関数によって返される値です。 (関数は関数の節で検討されている;配列は配列のセクションで考慮される ;学習のこの現在の段階では、定数を定数として扱い、変数を既に学習していると理解すれば十分である)。
オペレーション はオペランドに対して行われるアクションです。
操作シンボル は、操作を実行するために順序付けられたプリセット文字または 文字 グループです。
式 は、オペランドと演算記号のシーケンスです。 計算された値はデータ型によって特徴付けられるプログラムレコードです。
操作の種類
MQL4では、以下のタイプの操作が行われます。
• 算術
• 割り当て
• リレーショナル
• ブール
• ビット単位
• コンマ
• 関数呼び出し
オペレーションはオペレータで使用されます( オペレータを参照)。 演算子でのみ意味があり、プログラムで実現されます。 操作を使用する可能性は、操作者のプロパティによって決まります。オペレータのプロパティによってこの特定の操作を利用できる場合は、それを使用できます。 それ以外の場合は、この操作を使用しないでください。 オペレータ以外のオペレーションを使用することは禁止されています。
算術演算
次の記号は、算術演算記号です。
| シンボル | 操作 | 例 | アナログ |
|---|---|---|---|
| + | 値の加算 | x + 2 | |
| - | 値の減算または符号の変更 | x-3、y = -y | |
| * | 値の掛け算 | 3 * x | |
| / | 部門割当 | x / 5 | |
| % | 部門の残り | 分=時間%60 | |
| ++ | 変数の値に1を加算する | y ++ | y = y + 1 |
| - | 変数の値から1を引く | y- | y = y - 1 |
割り当て操作
以下のシンボルは、割り当て操作シンボルです。
| シンボル | 操作 | 例 | アナログ |
|---|---|---|---|
| = | 変数xへの値xの代入 | у= x | |
| + = | 変数yのx倍の増加 | у+ = x | y = y + x |
| - = | 変数yのxによる縮小 | y - = x | y = y - x |
| * = | 変数yとxの乗算 | y * = x | y = y * x |
| / = | xによる変数yの除算 | y / = x | y = y / x |
| %= | 変数yのxによる除算の剰余 | y%= x | y = y%x |
関係演算
以下の記号は、関係演算記号です。
| シンボル | 操作 | 例 |
|---|---|---|
| == | xがyに等しい場合は真 | x == y |
| != | xがyと等しくなければ真 | x!= y |
| < | xがyより小さければ真 | x <y |
| > | xがyより大きい場合は真 | x> y |
| <= | true、xがy以下の場合 | x <= y |
| > = | true、xがy以上の場合 | x> = y |
ブール(論理)演算
次のシンボルはブール演算記号です。
| シンボル | 操作 | 例 | 説明 |
|---|---|---|---|
| ! | NOT(論理否定) | ! х | オペランドの値がFALSE(0)の場合、TRUE(1)。 FALSE(0)、オペランドの値がFALSE(0)でない場合、 |
| || | OR(論理的論理和) | x <5 || x> 7 | TRUE(1)、値のいずれかの値がtrueの場合 |
| && | AND(論理連結) | x == 3 && y <5 | すべての値が真であればTRUE(1) |
ビット演算
ビット単位の演算は整数でしか実行できません。 次の操作はビット単位の操作です。
これは、 変数の値の 1の補数 を 返します 。 式の値には、変数の値に0が含まれるすべての場所に1が含まれ、変数の値に1が含まれるすべての場所に0が含まれます。
|
1 |
<span class="notranslate"> b =〜n;</span> |
xの バイナリ表現は 、 y 桁右 にシフトされ ます。 この右シフトは論理的です。 左に空になったすべての場所が0で埋められることを意味します。
|
1 |
<span class="notranslate"> x = x >> y;</span> |
xの バイナリ表現は 、 y 桁 だけ左にシフトされ ます。 左に空いた場所は0で埋められます。
|
1 |
<span class="notranslate"> x = x << y;</span> |
次の例 は、 x と yの バイナリ表現の AND 演算を示し てい ます。 式の値には、すべての場所で1(TRUE)が含まれます 。x と yの 両方 に0以外が含まれ、式の値には他のすべての場所で0(FALSE)が含まれます。
|
1 |
<span class="notranslate"> b =((x&y)!= <span class="number">0</span> );</span> |
次の例 は、 x と yの バイナリ表現の ビット演算 OR を示してい ます。 式の値には、すべての場所で1が含まれ、 x または yに は0が含まれません。他の場所には0が含まれます。
|
1 |
<span class="notranslate"> b = x |</span> <span class="notranslate"> y;</span> |
次の例 は、 x と yの バイナリ表現の 排他的論理和 を示してい ます。 式の値には、 x と yの バイナリ値が異なる 場所に1が格納され ます。 他の場所には0が入っています。
|
1 |
<span class="notranslate"> b = x ^ y;</span> |
コンマ操作
コンマで区切られた式は、左から右に計算されます。 左式の計算のすべての影響は、右式が計算される前に発生します。 結果のタイプと値は、正しい式のタイプと値と一致します。
|
1 |
<span class="notranslate"> <span class="keyword">for</span> (i = <span class="number">0</span> 、j = <span class="number">99</span> ; i < <span class="number">100</span> ; i ++、j--) <span class="functions">Print</span> (array [i] [j]);</span> <span class="notranslate"> <span class="comment">// Loop文</span></span> |
以下の転送パラメータリストを例として考えることができます。
|
1 |
<span class="notranslate"> My_function(Alf、Bet、Gam、Del) <span class="comment">//引数を持つ関数を呼び出す</span></span> |
演算子と関数の詳細については、この章の演算子と関数の節を参照してください。 詳細については、 演算子の章を参照してください。
関数呼び出し
関数呼び出しについては、 関数呼び出しの節で詳しく説明しています 。
類似のオペランドに対する操作
小学校の生徒に、鉛筆の数に関する問題を解決するときに、オペラント、オペレーター、表現などの言葉に基づいてプレゼンテーションを行う必要があると言われた場合、貧しい子供は確かにそれを不可能と感じるでしょう。 操作のシンボルを見ると、コーディングは神秘的で非常に複雑なプロセスであり、一種のエリートにしかアクセスできないと考えるかもしれません。 しかし、コーディングは本当に難しいことではありません。いくつかの意図を明確にするだけです。 これが本当にそうであることを確かめるために、いくつかの例を考えてみましょう。
| 問題1 Johnには2本の鉛筆があり、Peteには3本の鉛筆があります。 これらの少年は何本の鉛筆を持っていますか? 🙂 |
解1 Johnの鉛筆の数を変数 A 、Peteの鉛筆の数を変数 B とし、合計を Cとする 。
答えは Сです = А + Â 。
データ型セクションでは、変数宣言の方法を検討しました。 鉛筆は事物です。つまり、それは基本的に部品として存在することができます(例えば、鉛筆の半分があるかもしれません)。 したがって、ペンを実際の変数、つまり ダブルタイプの変数とみなします。
したがって、たとえば、次のようにソリューションをコーディングすることができます。
|
1 2 3 |
<span class="notranslate"> <span class="keyword">ダブル</span> A = <span class="number">2.0</span> ;</span> <span class="notranslate"> <span class="comment">//ジョンの鉛筆の数</span></span> <span class="notranslate"> <span class="keyword">二重</span> B = <span class="number">3.0</span> ;</span> <span class="notranslate"> <span class="comment">//ピートの鉛筆の数</span></span> <span class="notranslate"> <span class="keyword">ダブル</span> C = A + B;</span> <span class="notranslate"> <span class="comment">//総数</span></span> |
この場合、 同じデータ型の変数を一緒に加えることに適用される 操作 "+" を考慮することは非常に例示的 です。
次の式の値の型は、式の構成要素である変数の型になります。 私たちの場合、これはダブルタイプになります。
|
1 |
<span class="notranslate"> A + B</span> |
値の違いについても同様の答えが得られます。 ピートはジョンより何本持っていますか?
|
1 2 |
<span class="notranslate"> <span class="keyword">ダブル</span> A = <span class="number">2.0</span> ;</span> <span class="notranslate"> <span class="comment">//ジョンの鉛筆の数</span></span> <span class="notranslate"> <span class="keyword">ダブル</span> B = <span class="number">3.0</span> ;</span> <span class="notranslate"> <span class="comment">//ピートの鉛筆の数</span></span> |
他の算術演算も同様の方法で使用されます。
|
1 2 |
<span class="notranslate"> <span class="keyword">ダブル</span> C = B * A;</span> <span class="notranslate"> <span class="comment">// 2つの実数の乗算</span></span> <span class="notranslate"> <span class="keyword">ダブル</span> C = B / A;</span> <span class="notranslate"> <span class="comment">// 2つの実数の除算</span></span> |
整数でも同様の計算を行うことができます。
| 問題2 生徒は黒板に行き、授業で答えます。 ジョンは2回、ピートは3回行った。 男の子は何回黒板に通ったのですか? |
解2 Johnの節を変数 X 、ピートの節を変数 Y 、結果を Zとする 。
この例では、 int型の変数 を使用する必要 があります。なぜなら、それらの性質によって整数のイベントを考慮するからです。 たとえば、0.5倍または1.5倍の黒板に行くことはできません。 黒板での答えは良いか悪いかが問われますが、私たちはそのような答えや節の数にしか関心がありません。
この問題の解決方法は次のように書くことができます。
|
1 2 3 |
<span class="notranslate"> <span class="keyword">int</span> X = <span class="number">2</span> ;</span> <span class="notranslate"> <span class="comment">//ジョンのパッセージの数</span></span> <span class="notranslate"> <span class="keyword">int</span> Y = <span class="number">3</span> ;</span> <span class="notranslate"> <span class="comment">//ピートのパッセージの数</span></span> <span class="notranslate"> <span class="keyword">int</span> Z = X + Y;</span> <span class="notranslate"> <span class="comment">//総数</span></span> |
整数、整数の積、または整数の商の差異の計算の場合、適切な操作が同じ簡単な方法で使用されます。
|
1 2 3 4 5 |
<span class="notranslate"> <span class="keyword">int</span> X = <span class="number">2</span> ;</span> <span class="notranslate"> <span class="comment">//整数</span></span> <span class="notranslate"> <span class="keyword">int</span> Y = <span class="number">3</span> ;</span> <span class="notranslate"> <span class="comment">//整数</span></span> <span class="notranslate"> <span class="keyword">int</span> Z = Y - X;</span> <span class="notranslate"> <span class="comment">// 2つの整数の差</span></span> <span class="notranslate"> <span class="keyword">int</span> Z = Y * X;</span> <span class="notranslate"> <span class="comment">// 2つの整数の積</span></span> <span class="notranslate"> <span class="keyword">int</span> Z = Y / X;</span> <span class="notranslate"> <span class="comment">// 2つの整数の比</span></span> |
状況は、 文字列 型の 変数とは 少し異なり ます。
| 問題3 建物の一角に「北極」という食料品店があります。 同じ建物の別のコーナーには、「美容サロン」という施設があります。 建物には何が書かれていますか? |
解決策3 MQL4では、 文字列定数と変数の値を 一緒に追加することができ ます。 文字列型の変数を一緒に追加すると、文字列は、式で言及されている順序で1つずつ追加されます。
私たちに必要な答えを与えるプログラムをコーディングするのは簡単です。
|
1 2 3 |
<span class="notranslate"> <span class="keyword">文字列</span> W1 = <span class="string">"北極"</span> ;</span> <span class="notranslate"> <span class="comment">//文字列1</span></span> <span class="notranslate"> <span class="keyword">文字列</span> W2 = <span class="string">"美容院"</span> ;</span> <span class="notranslate"> <span class="comment">// String 2</span></span> <span class="notranslate"> <span class="keyword">文字列</span> Ans = W1 + W2;</span> <span class="notranslate"> <span class="comment">//文字列の合計</span></span> |
変数の値は、次のように表示される文字列になります。
|
1 |
<span class="notranslate"> ArcticHairdressing Saloon</span> |
私たち は文字列型の 値 を 得ました が、これは絶対に正しく形成されましたが、奇妙に見えます。 もちろん、そのような問題の実際のコーディングでは、ギャップやその他の句読点を考慮する必要があります。
文字列型の変数を使用するその他の算術演算は禁止されています。
|
1 2 3 |
<span class="notranslate"> <span class="keyword">文字列</span> Ans = W1-W2;</span> <span class="notranslate"> <span class="comment">//許可されません</span></span> <span class="notranslate"> <span class="keyword">文字列</span> Ans = W1 * W2;</span> <span class="notranslate"> <span class="comment">//許可されません</span></span> <span class="notranslate"> <span class="keyword">文字列</span> Ans = W1 / W2;</span> <span class="notranslate"> <span class="comment">//許可されません</span></span> |
型キャスト
型キャスティング は、 オペランドまたは式の値の型の変更(マッピング)です。 操作の実行 (代入操作を除く)の前に、変数は最も高い優先度のタイプに変更され、代入操作の実行前は変数がターゲットタイプに変更されます。
typecastingを扱ういくつかの問題を考えてみましょう。
| 問題4 Johnは2本の鉛筆を持っていますが、Peteは3回黒板に行きました。 合計でいくつですか? |
正式な論理に関する限り、問題の誤りは明らかです。 物事と一緒に出来事を加えることができないという理由があります。 違います。
| 問題5 家の一角には「北極」という食料品店があり、ジョンには2本の鉛筆があります。 🙂 |
絶望の程度で(通常の推論が関係する限り)、「合計で何人ですか?」と聞くことができます。 あるいは、「家には何が書かれていますか?」と聞くことができます。 しかし、我々は両方の質問をすることはできません。
上記の両方の問題をMQL4で正しく解決したい場合は、型キャスト規則を参照する必要があります。 まず、さまざまなタイプの変数がどのようにコンピュータメモリに表現されているかについて話をする必要があります。
データ 型 int、bool、color、datetime、およびdoubleは数値データ型に属します。 これらの型の定数と変数の内部表現は数字です。 int型、bool型、colour型、およびdatetime型の変数は、コンピュータメモリに整数として表されますが、double型の変数は浮動小数点数を持つ倍精度の数値、つまり実数で表されます。 文字列型の定数と変数の値は文字の集合 です(図16参照)。
| int型、bool型、color型、およびdatetime型の値は、コンピュータメモリに整数として表されます。 ダブルタイプの値は、コンピュータメモリ内で実数として表されます。 文字列型の値は、一連の文字としてコンピュータメモリに表されます。 int型、bool型、color型、datetime型、double型の値は、数値型の値です。 文字列型の値は文字型の値です。 |
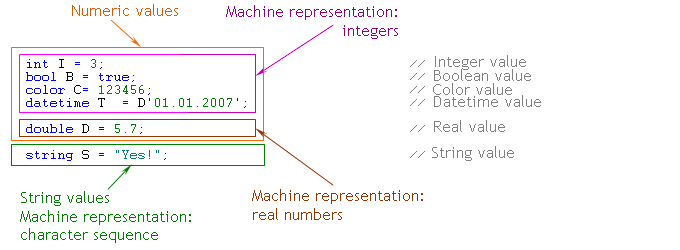
図16 コンピュータメモリ内の異なるデータ型の表現。
int、bool、color、およびdatetime型の変数の 値は、 整数としてコンピュータメモリに表されていますが、double型の変数の値は実数として表されています。 したがって、異なる型の変数で構成される式の型を調べたい場合、int、double、およびstringという3つのデータ型から選択できます。 bool、color、およびdatetime型の値は、int型の値と同じ方法で式に自身を証明します。
したがって、異なる型のオペランドで構成される式の値はどのような型になりますか? MQL4では、 暗黙の型キャスティングの ルール が受け入れられます。
| •式 に異なる型のオペランドが含まれて いる場合 、式の型は最も優先度の高い型に変換されます。 int型、bool型、color型、datetime型の優先度は同じですが、double型の方が優先度が高く、文字列型の優先度が最も高くなります。
• 代入演算記号の右の式の型が代入演算記号の左の変数の型と一致しない場合、この式の値は変数の型として左にキャストされます割当て操作標識。 これは「ターゲットタイプキャスト」と呼ばれます。 • 文字列 型の 値を 他の任意の型に キャストすることは禁止されてい ます。 |
問題4に戻りましょう。それには2つの解決策があります。
解答4.1 結果をint型の値として計算することができます。
|
1 2 3 |
<span class="notranslate"> <span class="keyword">ダブル</span> A = <span class="number">2.0</span> ;</span> <span class="notranslate"> <span class="comment">//ジョンの鉛筆の数</span></span> <span class="notranslate"> <span class="keyword">int</span> Y = <span class="number">3</span> ;</span> <span class="notranslate"> <span class="comment">//ピートのパッセージの数</span></span> <span class="notranslate"> <span class="keyword">int</span> F = A + Y;</span> <span class="notranslate"> <span class="comment">//総数</span></span> |
まず 、式の値を知る必要があります。ただし、そのオペランドの型が異なっていなければなりません。 次の式では、2つのデータ型のオペランドが使用されます。 А はdouble、 Y はintです。
|
1 |
<span class="notranslate"> A + Y</span> |
暗黙の型キャストの規則に従って、この式の値 は double 型の 数になり ます。 式 A + Yの 型についてのみ話 していますが、代入演算記号の左にある 変数 Fの 型 については話して いません 。 この式の値は実数5.0です。 式 A + Yの 型をキャストするため に、暗黙の型キャスト規則の最初の部分を適用しました。
式 A + Yの計算の 後、割当て操作が実行される。 この場合、型の不一致もあります。 式A + Yの型は double 型であり、変数 Fの 型 は int型 です。 代入演算の実行中、式 A + Y の型はint型 (整数計算の規則に従って) としてキャストさ れ、整数5になります。 この結果は、整数変数 Fの 値になり ます。 計算は、暗黙の型キャスト規則の第2部であるターゲット型キャストに従って実行されています。 計算と操作の最終結果は整数変数 Fの 値 が整数5であることです。
解答4.2 double 型の 値として結果を得ようとすると、同様の状況が発生し ます。
|
1 2 3 |
<span class="notranslate"> <span class="keyword">ダブル</span> A = <span class="number">2.0</span> ;</span> <span class="notranslate"> <span class="comment">//ジョンの鉛筆の数</span></span> <span class="notranslate"> <span class="keyword">int</span> Y = <span class="number">3</span> ;</span> <span class="notranslate"> <span class="comment">//ピートのパッセージの数</span></span> <span class="notranslate"> <span class="keyword">二重</span> F = A + Y;</span> <span class="notranslate"> <span class="comment">//総数</span></span> |
この状況は 、代入演算記号の左側に ある変数 Fの ターゲットタイプが式 A + Yの タイプと一致する ダブル タイプである ため、ターゲットタイプキャストを持たないという点で前のものとは異なりますここに。 計算の結果( double 型変数Fの値)は、実数5.0です。
ここで、問題5の解を見てみましょう。変数の初期化時に質問は出ません。
|
1 2 |
<span class="notranslate"> <span class="keyword">文字列</span> W1 = <span class="string">"北極"</span> ;</span> <span class="notranslate"> <span class="comment">//文字列1</span></span> <span class="notranslate"> <span class="keyword">二重</span> A = <span class="number">2</span> ;</span> <span class="notranslate"> <span class="comment">//ジョンの鉛筆の数</span></span> |
解決策5.1 これは、この問題の解決策です。
|
1 2 3 |
<span class="notranslate"> <span class="keyword">文字列</span> W1 = <span class="string">"北極"</span> ;</span> <span class="notranslate"> <span class="comment">//文字列1</span></span> <span class="notranslate"> <span class="keyword">二重</span> A = <span class="number">2</span> ;</span> <span class="notranslate"> <span class="comment">//ジョンの鉛筆の数</span></span> <span class="notranslate"> <span class="keyword">文字列</span>合計= W1 + A;</span> <span class="notranslate"> <span class="comment">//右への暗黙の変換</span></span> |
ここでは、右側の部分に、 文字列型とdouble型の 2つの変数の値をまとめてい ます。 暗黙の型キャスティングのルールによれば、変数 Aの 値 は最初に文字列型にキャストされます(この型は優先度が高いため)。 次に等価値が加算されます。 代入演算記号の右側の結果の値は新しい文字列になります。 文字列を一緒にストリングするこのプロセスは、連結と呼ばれ ます。 次の段階で、この値は文字列変数 Sumに 割り当てられ ます。 その結果、変数 Sumの 値は 次の文字列になります。
|
1 |
<span class="notranslate">北極2。</span> <span class="notranslate"> <span class="number">00000000</span></span> |
解決策5.2 以下の解決策は間違っています。
|
1 2 3 |
<span class="notranslate"> <span class="keyword">文字列</span> W1 = <span class="string">"北極"</span> ;</span> <span class="notranslate"> <span class="comment">//文字列1</span></span> <span class="notranslate"> <span class="keyword">二重</span> A = <span class="number">2</span> ;</span> <span class="notranslate"> <span class="comment">//ジョンの鉛筆の数</span></span> <span class="notranslate">ダブルサム= W1 + A;</span> <span class="notranslate"> <span class="comment">//これは許されない</span></span> |
この場合、 文字列 型の 値のターゲット型キャストを禁止し ます。 式 W1の 値の型 + 前の例のように、暗黙の型キャストのため、 A は 文字列 です。 割り当て操作が実行されると、ターゲットの型キャストが実行されなければなりません。 ただし、ルールに従って、文字列型の式を優先度の低い型にキャストできません。 これは、プログラムの作成時に、つまりコンパイル時にMetaEditorによって検出されるエラーです。
一般に、このセクションで与えられた規則は明確かつ単純です。 値を計算する場合は、すべての異なるタイプを最高の優先順位を持つタイプにキャストする必要があります。 優先度を下げた型キャストは数値に対してのみ許可されますが、文字列は数値に変換できません。
整数計算の特徴
整数は小数部分のない数値です。 それらを一緒に追加したり減算したりすると、わかりやすい結果が得られます。 たとえば、次のことが当てはまるとします。
|
1 2 |
<span class="notranslate"> <span class="keyword">int</span> X = <span class="number">2</span> ;</span> <span class="notranslate"> <span class="comment">//最初のint変数</span></span> <span class="notranslate"> <span class="keyword">int</span> Y = <span class="number">3</span> ;</span> <span class="notranslate"> <span class="comment">// 2番目のint変数</span></span> |
そして、以下が真であると仮定します。
|
1 |
<span class="notranslate"> <span class="keyword">int</span> Z = X + Y;</span> <span class="notranslate"> <span class="comment">//加算演算、</span></span> |
この場合、変数 Z :2 + 3 = 5の 値を計算するのに問題はありません 。
同様に、次の乗算演算を実行します。
|
1 |
<span class="notranslate"> <span class="keyword">int</span> Z = X * Y;</span> <span class="notranslate"> <span class="comment">//乗算演算、</span></span> |
結果は非常に予測可能です:2 * 3 = 6。
しかし、プログラムで除算演算を実行する必要がある場合、どのような結果が得られますか?
|
1 |
<span class="notranslate"> <span class="keyword">int</span> Z = X / Y;</span> <span class="notranslate"> <span class="comment">//除算演算</span></span> |
2/3を書くのは簡単です が、整数ではありません。 したがって、 式Xの 値はどうなりますか / Y と変数 Z ?
| 整数計算のルールは、小数部分は常に破棄されるということです。 |
上記の例では、等号の右側の式には整数のみが含まれています。つまり、型キャストは行われません。 そして、これは、式 Xの タイプ / Y はintです。 したがって、 式Xの 整数値を求めた結果 / Y (2 / 3)は0(ゼロ)である。 この値(ゼロ)は 、最後 に変数 Z に割り当てられ ます。
これに対応して、変数 X および Y の他の値は 他の結果を生じる。 たとえば、次のコード行で は、式 X の7/3の 値 / Y と変数 Z は2に等しい。
|
1 2 3 |
<span class="notranslate"> <span class="keyword">int</span> X = <span class="number">7</span> ;</span> <span class="notranslate"> <span class="comment">// int変数の値</span></span> <span class="notranslate"> <span class="keyword">int</span> Y = <span class="number">3</span> ;</span> <span class="notranslate"> <span class="comment">// int変数の値</span></span> <span class="notranslate"> <span class="keyword">int</span> Z = X / Y;</span> <span class="notranslate"> <span class="comment">//除算演算、</span></span> |
オペレーションの順序
計算ルールは次のとおりです。
| 式の値は、算術演算の優先順位に従って計算され、左から右へ、各中間結果は型キャスト規則に従って計算されます。 |
次の例の式の計算順序を考えてみましょう。
|
1 |
<span class="notranslate"> Y = <span class="number">2.0</span> *( <span class="number">3</span> * X / Z-N)+ D;</span> <span class="notranslate"> <span class="comment">//例示的な表現</span></span> |
等号の右側の式は、2.0 * (3 バツ / Z - N )および D。 summand 2.0 * (3 バツ / Z - N )は2つの要素、すなわち2と(3 * バツ / Z - N )。 カッコ内の表現、3 * X / Z - N は、2つの和集合からなる。 サマンド3 * X / Z は3つの因子、すなわち3、 X、 Zからなる 。
等号の右側の式を計算するために、まず式3の値を計算し ます バツ / Z。 この式には同じランクの2つの演算(乗算と除算)が含まれているため、この式を左から右に計算します。 まず、式3の値を計算し ます X 、この式の型は変数 Xの 型と同じ です。 次に、式3の値を計算し ます* バツ / Z 型は、型キャスト規則に従って計算されます。 その後、プログラムは式の値と型を計算します3 * バツ / Z - Nを計算します。 次に、2.0 * (3 * バツ / Z - N )。 最後に、式2.0 * (3 * バツ / Z - N ) + D。
簡単に分かるように、プログラム内の演算の順序は数学の場合と似ています。 しかし、プログラムでは、中間結果の値の種類を考慮する必要があります。中間結果は、計算の最終結果に大きな影響を与えます。 特に、式中のオペランドの順序は非常に重要です(数学で受け入れられる規則とは異なります)。 これを実証するために、小さな例を考えてみましょう。
| 問題6 式の値を計算する / Â * С と А * С / Â 整数 А 、 В 、および Сの場合 。 |
計算の結果は、どちらの場合も同じであると直感的に予想されます。 しかし、この文は実数に対してのみ真です。 int型のオペランドで構成される式の値を計算すると、中間結果を常に考慮する必要があります。 オペランドのシーケンスは基本的に重要です。
|
1 2 3 4 5 |
<span class="notranslate"> <span class="keyword">int</span> A = <span class="number">3</span> ;</span> <span class="notranslate"> <span class="comment">// int型の値</span></span> <span class="notranslate"> <span class="keyword">int</span> B = <span class="number">5</span> ;</span> <span class="notranslate"> <span class="comment">// int型の値</span></span> <span class="notranslate"> <span class="keyword">int</span> C = <span class="number">6</span> ;</span> <span class="notranslate"> <span class="comment">// int型の値</span></span> <span class="notranslate"> <span class="keyword">int</span> Res_1 = A / B * C;</span> <span class="notranslate"> <span class="comment">//結果0(ゼロ)</span></span> <span class="notranslate"> <span class="keyword">int</span> Res_2 = A * C / B;</span> <span class="notranslate"> <span class="comment">//結果3(3)</span></span> |
式 A を計算するプロセスに従ってみましょう / B * C :
まず、左から右へ、式 A / B が計算されます。 上記の規則によれば、式(3 / 5)は整数0(ゼロ)です。
2.式0 * С (ゼロを掛けたゼロ )を計算すると、整数は0(ゼロ)になります。
3.一般的な結果(変数 Res_1の 値 )は整数0(ゼロ)です。
ここで、 A * C / Bの 式を計算することの発展に従ってみましょう 。
A * Cの計算 は、 整数18(3 * 6 = 18)を生成する。
式18の計算 / B は 明らかな答えを出します。 小数部分が破棄された後、(18 / 5)は整数3(3)です。
3.一般的な結果(変数 Res_2の 値 )は整数3(3)です。
前の例では、int型の変数の値が計算されるちょうど小さなコード断片を検討しました。 これらの変数を同じ値の定数に置き換えると、最終的な結果は同じになります。 整数を含む式を計算するときは、プログラム行の内容にもっと注意を払う必要があります。 そうしないと、コードにエラーが発生する可能性があります。これは、特に大規模なプログラムでは、後で見つけて修正するのが非常に難しくなります。 このような問題は、実数を使用した計算では発生しません。 ただし、1つの複合式で異なるタイプのオペランドを使用する場合、最終結果は、整数の除算を含むランダムに形成されたフラグメントに完全に依存する場合があります。
演算子セクションでは、 演算子の用語と一般的なプロパティが考慮されますが、各演算子の特殊プロパティは演算子という章で説明されています。